Het warmtegetal is een maat voor de warmte in het tijdvak van 1 april tot en met 31 oktober van het genoemde jaar. Het warmtegetal wordt berekend door het aantal graden dat de gemiddelde etmaaltemperatuur van elke dag boven de 18,0 °C ligt, op te tellen. Een dag met gemiddeld over 24 uur een temperatuur van 20,2 °C draagt dus 2,2 bij aan het warmtegetal. Zo komen we uiteindelijk tot een totale som die het mogelijk maakt de warmte in het jaar te classificeren.
Actuele stand 2014: 90.7 (t/m 31 oktober)
Links gesorteerd op jaartal, rechts op warmtegetal
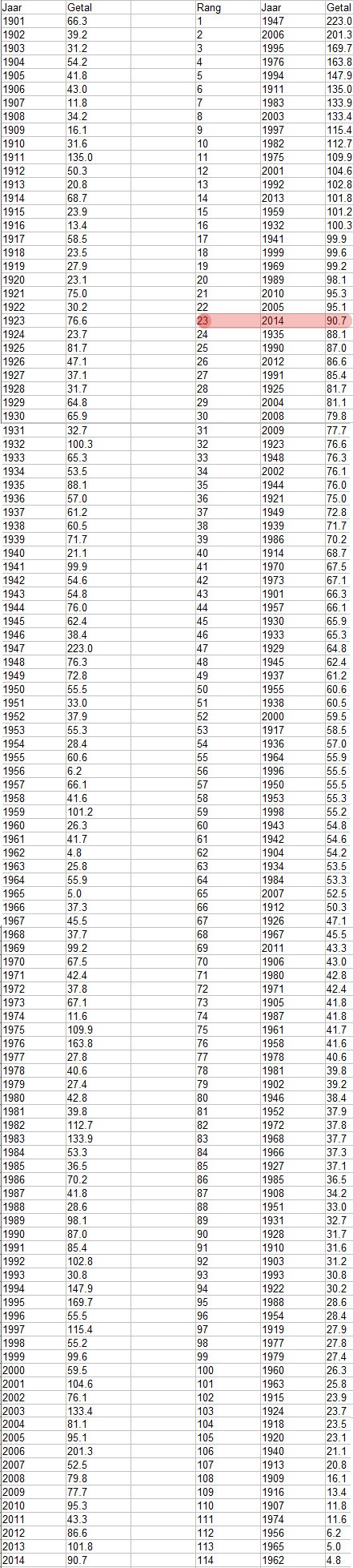
Bron:KNMI | Gewijzigd: 1 november 2014, 17:26 uur, door Ben47
Extreme warmte zoals in 1947 zorgde dus voor een eerste plaats terwijl de wintermaanden tot de allerkoudste ooit worden gerekend...( op die van 1963 na dan )
1947: de zomer van de 20e eeuw
16 juli 2006 - De laatste jaren maken we de ene na de andere warme zomer mee, maar topzomer in ruim honderd jaar is nog steeds die van 1947. In De Bilt kwam de gemiddelde temperatuur uit op 18,7 graden tegen 16,6 normaal (gemiddeld over 1971-2000).
Niet alleen in ons land maar ook in andere delen van Europa was dit de warmste zomer van de 20e eeuw. Daarna zijn er nog zes zeer warme zomers geweest (1976, 1983, 1994, 1995, 1997 en 2003) met een gemiddelde temperatuur van 18,0 graden en hoger. De zomer van 1947 is echter niet meer overtroffen en heeft nog steeds het predikaat "zomer van de eeuw". Die zomer begon al op 8 mei en duurde vrijwel zonder onderbreking tot 21 september. Het ene record na het andere sneuvelde en de natuur heeft, ook omdat de zomer voorafgegaan werd door één van de strengste winters van de 20e eeuw, laten zien waartoe ons klimaat in staat is.
source : http://www.knmi.nl/cms/content/6116/1947_de_zomer_van_de_20e_eeuw
De spectaculaire winter van 1947
De vele koude periodes maakten de winter van 1946-1947 zeer indrukwekkend, zeker naar onze huidige maatstaven. Met een gemiddelde temperatuur van -2,4 °C in De Bilt is deze winter op die van 1963 na de koudste van de twintigste eeuw.
source : www.knmi.nl
Winter in Volendam in 1947
source: http://kanaalridder.blogspot.nl/2011_12_01_archive.html

Dit geeft eigenlijk mooi aan hoe moeilijk het is om een maatstaf te vinden over een jaar. Net als de Hellmangetallen zijn er vele haken en ogen aan tabellen als deze en moet je altijd iets verder kijken dan alleen naar een gemiddelde om een totaal analyse te kunnen doen over een periode. Maar goed als je hieronder verder leest dan zie je ook dat je "het Warmtegetal" niet moet gebruiken voor uitspraken over het hele jaar.
Als je de hellman getallen erbij zou betrekken ( winter 1947 342,8 Hellmannen ( 2de plek !) dan zou je de Hellmannen als een negatief getal kunnen gebruiken..
- warmtegetal 1947 is 223 - 342,8 = minus 119,8
- warmtegetal 2014 is 90,7 - 0 = plus 90, 7
Goed deze berekening is natuurlijk een beetje creatief want deze winter was natuurlijk van nov 46 mrt 47 maar het geeft wel aan dat je altijd goed moet kijken waar een getal voor staat. Je kan het bovenstaande nog iets geloofwaardiger maken door de hellmannen per maand te gebruiken zodat je ook binnen het jaar blijft. (al maakt dat voor deze winter niet veel uit want de strengste periode van koude was in jan -mrt 1947 ( inclusief elfstedentocht)
Maar goed ik denk dat mijn punt wel staat
Even wat huiswerk gedaan:
Het warmtegetal is eigenlijk de zomervariant van Hellman.. Dus dit getal moet niet gebruikt worden om iets te zeggen over verlopen jaar ( 2014 bijvoorbeeld) omdat de de Hellman wintermaanden niet worden meeberekend.
Nog wat input van het KNMI:
Het warmtegetal voor de zomer is de tegenhanger van het koudegetal dat voor de winter wordt gebruikt en dat van alle dagen met een etmaalgemiddelde onder nul de negatieve waarde van de temperatuur sommeert. Het warmtegetal geeft alleen een indruk van de warmte in het zomerhalfjaar.
Om een totale indruk te krijgen van de kwaliteit van het zomerweer moeten ook andere grootheden, zoals regen en zon, meegenomen worden. Daarvoor zijn andere methodes in gebruik zoals het in kaart brengen van het aantal mooi-weerdagen, ook wel aangeduid als ADS-dagen. Dat zijn dagen met een gemiddelde temperatuur ruim boven wat voor de tijd van het jaar normaal is (decadegemiddelde), hooguit 0,2 mm neerslag en een zonneschijnduur van minstens 50 procent.
als je zelf wilt lezen : http://www.knmi.nl/cms/content/21584/warmtegetal | Gewijzigd: 2 november 2014, 23:37 uur, door Callie-P

De spectaculaire winter van 1947
De vele koude periodes maakten de winter van 1946-1947 zeer indrukwekkend, zeker naar onze huidige maatstaven. Met een gemiddelde temperatuur van -2,4 °C in De Bilt is deze winter op die van 1963 na de koudste van de twintigste eeuw.
Dit geeft eigenlijk mooi aan hoe moeilijk het is om een maatstaf te vinden over een jaar. Net als de Hellmangetallen zijn er vele haken en ogen aan tabellen als deze en moet je altijd iets verder kijken dan alleen naar een gemiddelde om een totaal analyse te kunnen doen over een periode. Maar goed als je hieronder verder leest dan zie je ook dat je "het Warmtegetal" niet moet gebruiken voor uitspraken over het hele jaar.
Als je de hellman getallen erbij zou betrekken ( winter 1947 342,8 Hellmannen ( 2de plek !) dan zou je de Hellmannen als een negatief getal kunnen gebruiken..
- warmtegetal 1947 is 223 - 342,8 = minus 119,8
- warmtegetal 2014 is 90,7 - 0 = plus 90, 7
Goed deze berekening is natuurlijk een beetje creatief want deze winter was natuurlijk van nov 46 mrt 47 maar het geeft wel aan dat je altijd goed moet kijken waar een getal voor staat. Je kan het bovenstaande nog iets geloofwaardiger maken door de hellmannen per maand te gebruiken zodat je ook binnen het jaar blijft. (al maakt dat voor deze winter niet veel uit want de strengste periode van koude was in jan -mrt 1947 ( inclusief elfstedentocht)
Maar goed ik denk dat mijn punt wel staat
Even wat huiswerk gedaan:
Het warmtegetal is eigenlijk de zomervariant van Hellman.. Dus dit getal moet niet gebruikt worden om iets te zeggen over verlopen jaar ( 2014 bijvoorbeeld) omdat de de Hellman wintermaanden niet worden meeberekend. In de eerste zin van mijn eerste bericht over Warmtegetallen staat reeds dat het niet het hele jaar betreft, nog de zomer (JJA) maar het tijdvak april t/m oktober! Dus daar had je geen huiswerk voor hoeven te doen!!
Dus je kan je er niets mee voor een heel kalender jaar en dat wordt ook nergens beweerd! Je kan er alleen andere jaren met dezelfde periode mee vergelijken en zo is de tabel van KNMI dan ook opgebouwd.
Hellmannen er vanaf trekken is het aantal peren van het aantal appels aftrekken en slaat nergens op.
Hoogstens zou je voor de grap de beide getallen bij elkaar kunnen optellen (hetgeen ook op appels en peren optellen lijkt) om een indruk te krijgen van het extreme karakter van een (niet kalender)jaar. Dus zo'n EXTREEMINDEX jaar loopt dan voor 1947 van 1 november 1946 t/m 31 oktober 1947. (Ik kies hiervoor omdat aaneensluitende winter en zomer bij elkaar beoordeeld worden en is practisch aangezien de hellmanngetallen ook over de hele winterperiode bekend zijn)
1e Extreemindex wordt dan 1947 met 565,8
1963 komt op 345,9 + 25,8 = 371,7
Ik heb niet alle jaren bekeken, maar geloof niet dat er ook maar 1 in de buurt komt van 1947.
Kortom:
De gemiddelde temperatuur kan in een maand hoog zijn (bijv juni 18 graden i.p.v. normaal 15,6 graden), maar het aantal etmalen (en daarvan de hoeveelheid graden) boven de 18 kan laag zijn..Dan is het een warme maand, maar met een laag warmtegetal. Bij Hellmann hetzelfde. Als alle 31 etmalen van januari afzonderlijk gemiddeld op 0 graden uitkomen heb je met een maandgemiddelde van 0 graden een behoorlijk koude januari want het normaalgemiddelde voor die maand is +3,1. Het aantal Hellmannpunten is echter 0,0.
Dus Warmtegetallen en Hellmanngetallen geven de mate van extremiteit van etmalen aan in de voor deze geldende tijdvakken van het jaar Een zeer koude april of oktoberdag met een etmaaltemperatuur onder 0 valt buiten de Hellmann, evenals de etmaaltemperatuur van boven de 18 graden in maart of november buiten de warmtegetallen valt. Maar ze tellen natuurlijk wel mee voor de gemiddelde maandtemperatuur, gemiddelde enz enz..

 2014 niet zo warm volgens Warmtegetallen sinds 1901 in De Bilt
2014 niet zo warm volgens Warmtegetallen sinds 1901 in De Bilt




